Олимпиадная задача по планиметрии для 8-9 класса: ΔABC с ∠B=120°, авторы Акопян, Швецов
Задача
Дан равнобедренный треугольник ABC, в котором ∠B = 120°. На продолжениях сторон AB и CB за точку B взяли точки P и Q соответственно так, что лучи AQ и CP пересекаются под прямым углом. Докажите, что ∠PQB = 2∠PCQ.
Решение
Выберем на луче BC такие точки X и P', что BX = BP, BP' = BP + BQ. Тогда треугольник BPX – равнобедренный с углом 60°, то есть равносторонний, и PX = BP, ∠PXP' = 120°. Значит, треугольники PBQ и PXP' равны по двум сторонам и углу между ними, поэтому PP' = PQ и ∠PP'B = ∠PQB. Аналогично, выбрав на луче BA точку Q' так, что BQ' = BP + BQ, получаем, что QQ' = QP и ∠QQ'B = ∠QPB (см. рис.).
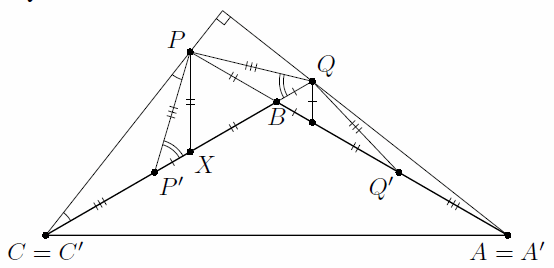
BA' = BQ' + Q'A' = BP + BQ + PQ = BP' + P'C' = BC'. Треугольники QQ'A' и PP'C' равнобедренные, поэтому
∠Q'A'Q + ∠P'C'P = ½ (∠QQ'B + ∠PP'B) = ½ (∠BPQ + ∠BQP) = 30╟. Значит, угол между прямыми QA' и PC' равен
180° – (∠Q'A'Q + ∠P'C'P + ∠BA'C' + ∠BC'A') = 90°. Но, если BA' = BC' < BA, то этот угол должен быть меньше 90°, а если BA' > BA, то больше. Значит,
A' = A, C' = C, и ∠PQB = ∠PP'B = 2∠PCP' = 2∠PCQ.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь