Назад

Олимпиадная задача по планиметрии: угол AKC в треугольнике для 8-9 классов

Задача 216895 • Сложность: 2 • 8-9 класс
Задача

Точка M – середина основания AC остроугольного равнобедренного треугольника ABC. Точка N симметрична M относительно BC. Прямая, параллельная AC и проходящая через точку N, пересекает сторону AB в точке K. Найдите угол AKC.

Авторы:
Блинков А. Д.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
4
Решение

Пусть L – точка пересечения NK и BC (см. рис.).

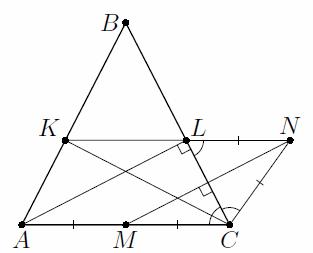
Ясно, что  AM = MC = CN  и  ∠MCB = ∠NCB.  Но и  ∠CLN = ∠LCM  (поскольку  LN || AC),  а значит, треугольник CNL равнобедренный, и

LN = CN = AM.  Следовательно, отрезки AM и LN параллельны и равны, поэтому ALNM – параллелограмм, и  AL || MN ⊥ LC.  Наконец, из симметрии треугольника относительно высоты BM получаем  ∠AKC = ∠ALC = 90°.

Ответ

90°.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет