Олимпиадная задача по планиметрии: инцентр треугольника и вписанные окружности (8–9 класс)
Задача
Дан треугольник ABC. Пусть I – центр его вписанной окружности, и пусть X, Y, Z – центры вписанных окружностей треугольников AIB, BIC и AIC соответственно. Оказалось, что центр вписанной окружности треугольника XYZ совпадает с I. Обязательно ли тогда треугольник ABC равносторонний?
Решение
Пусть K – точка пересечения отрезков XY и BI, L – отрезков YZ и CI, а M – отрезков XZ и AI. По условию отрезок XI делит пополам углы KIM и KXM, поэтому треугольники IKX и IMX равны. Аналогично равны треугольники IKY и ILY, ILZ и IMZ. Следовательно,
∠IKY = ∠ILY = 180° – ∠ILZ = 180° – ∠IMZ = ∠IMX = ∠IKX, то есть BI ⊥ XY.
В треугольнике XBY отрезок BK служит биссектрисой и высотой, а значит, и медианой, то есть прямая BI – серединный перпендикуляр к отрезку XY. Поэтому ∠XIK = ∠YIK. Но ∠XIK = ½ ∠AIB = ½ (90° + ½ ∠C), а ∠YIK = ½ (90° + ½ ∠A) (см. задачу 155448). Следовательно, ∠A = ∠C. Аналогично ∠A = ∠B.
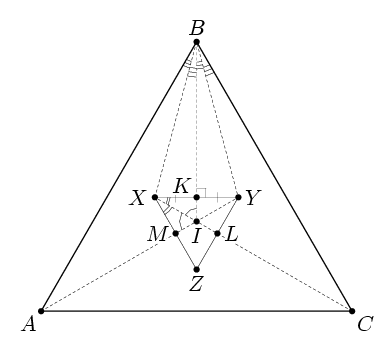
Ответ
Обязательно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь