Олимпиадная задача по алгебре и теории чисел для 8-9 класса: плюсы на диагонали квадрата 11×11
Задача
В некоторых клетках квадрата 11×11 стоят плюсы, причём всего плюсов чётное количество. В каждом квадратике 2×2 тоже чётное число плюсов.
Докажите, что чётно и число плюсов в 11 клетках главной диагонали квадрата.
Решение
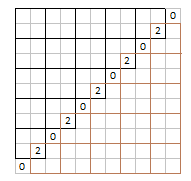
Ступенчатая фигура в левом верхнем углу (см. рис.) состоит из квадратиков 2×2, поэтому в ней чётное число плюсов. То же верно для фигуры в правом нижнем углу. Сложив эти числа, мы получим чётное число. При этом плюс в каждой из клеток квадрата вне диагонали учтён один раз, а в каждой клетке диагонали – 0 или 2 раза. Значит, число плюсов вне диагонали чётно. А так как чётно общее число плюсов, то и на диагонали число плюсов чётно.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет