Назад

Олимпиадная задача по планиметрии для 5–7 класса: углы и биссектрисы в треугольнике

Задача 216791 • Сложность: 2 • 5-7 класс
Задача

Внутри угла AOB, равного 120°, проведены лучи OC и OD так, что каждый из них является биссектрисой какого-то из углов, получившихся на чертеже. Найдите величину угла AOC, указав все возможные варианты.

Разделы:
Планиметрия
Источники:
Окружная олимпиада (Москва) Олимпиады и турниры 2010 год 7 класс
Количество версий:
4
Решение

Возможные расположения лучей показаны на рисунках.

                             
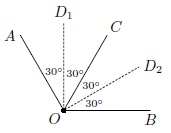
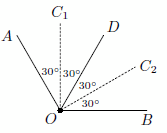
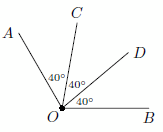
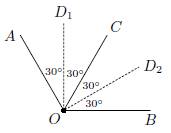
  1) Если лучOCявляется биссектрисой углаAOB(рис. слева), то  ∠AOC= 60°  (независимо от того, является ли лучODбиссектрисой углаAOCили углаBOC).   2) Если лучODявляется биссектрисой углаAOB, то  ∠AOC= 30°  (еслиOC– биссектриса углаAOD) или  ∠AOC= 90°  (еслиOC– биссектриса угла ∠BOD)   3) Если лучOC– биссектриса углаAOD, а лучOD– биссектриса углаBOC, то  ∠AOC= 60°.   4) Аналогично если лучOD– биссектриса угла ∠AOC, а лучOC– биссектриса углаBOD(рис. справа), то  ∠AOC= 80°.
Ответ

30°, 40°, 60°, 80° или 90°.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет