Назад

Олимпиадная задача по планиметрии: центры окружностей в треугольнике (10-11 класс)

Задача 216776 • Сложность: 3 • 10-11 класс
Задача

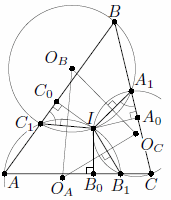
Точки A1, B1, C1 выбраны на сторонах BC, CA и AB треугольника ABC соответственно. Оказалось, что  AB1 – AC1 = CA1 – CB1 = BC1 – BA1.  Пусть OA, OB и OC – центры описанных окружностей треугольников AB1C1, A1BC1 и A1B1C. Докажите, что центр вписанной окружности треугольника OAOBOC совпадает с центром вписанной окружности треугольника ABC.

Авторы:
Полянский А.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2011-2012 Заключительный этап
Количество версий:
4
Решение

  Обозначим через I центр вписанной окружности треугольника ABC, а через A0, B0, C0 – точки её касания со сторонами BC, CA, AB. Будем считать, что точка A1 лежит на отрезке A0B. Как и в задаче 116760 (способ 1) докажем, что четырёхугольники BC1IA1, AB1IC1 и CA1IB1 вписаны, и  IA1 = IB1 = IC1.

  Линии центров OBOC, OCOA, OAOB являются серединными перпендикулярами к общим хордам IA1, IB1, IC1 соответственно; длины этих хорд равны. Значит, расстояния от I до сторон треугольника OAOBOC равны. Поскольку углы IBA1 и ICA1 острые, а точка A1 лежит на отрезке BC, то линия центров OBOC пересекает общую хорду IA1. Аналогично пересекаются отрезки OAOC и IB1, OAOB и IC1. Значит, I лежит внутри треугольника OAOBOC, то есть является центром его вписанной окружности.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет