Олимпиадная задача по многочленам и теории графов для 10-11 класса Шаповалова
Задача
Изначально на доске были написаны одночленs 1, x, x², ..., xn. Договорившись заранее, k мальчиков каждую минуту одновременно вычисляли каждый сумму каких-то двух многочленов, написанных на доске, и результат дописывали на доску. Через m минут на доске были написаны, среди прочих, многочлены S1 = 1 + x, S2 = 1 + x + x², S3 = 1 + x + x² + x3, ..., Sn = 1 + x + x² + ... + xn. Докажите, что 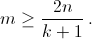
Решение
Построим граф, соответствующий конечной ситуации на доске: если многочлен P появился как сумма многочленов Q и R, то проведём стрелки из P в Q и R. Если из многочлена F ведёт ориентированный путь в G, будем говорить, что G участвует в F (в частности, сам F участвует в F). Нетрудно видеть в этом случае, что все коэффициенты многочлена F – G неотрицательны.
Можно считать, что каждый многочлен на доске – сумма различных степеней x: если какой-то коэффициент многочлена не меньше 2, то и у всех, в которых он участвует, соответствующий коэффициент также будет не меньше 2. Значит, он не участвует в суммах вида Si.
Каждый из многочленов S1, ..., Sn назовём финальным. Каждый из многочленов, участвующих в Sn (то есть в сумме всех исходных одночленов), назовём существенным.
Покажем индукцией по p, что в многочлене с p ненулевыми коэффициентами участвуют ровно 2p – 1 многочленов (из которых p одночленов); отсюда будет следовать, что количество существенных многочленов равно 2n + 1. База (p = 1) очевидна.
Шаг индукции. Пусть многочлен P был получен на некотором шаге как сумма Q и R, и количества ненулевых коэффициентов в P, Q и R равны p, q и r соответственно; тогда p = q + r. По предположению индукции, в Q и R участвуют 2q – 1 и 2r – 1 многочленов, среди которых нет совпадающих (поскольку в Q и R нет общих одночленов). Тогда в P, с учётом самого P, участвуют (2q – 1) + (2r – 1) + 1 = 2p – 1 многочленов.
Покажем, что в каждую минуту на доске появлялось не более одного финального существенного многочлена. Действительно, пусть в некоторый момент появились одновременно существенные многочлены Sp и Sq (p < q). Рассмотрим первый момент, когда на доске появился многочлен P, в котором одновременно участвуют и Sp и Sq; тогда он появился как сумма двух многочленов, каждый из которых содержит одночлен xp. Но тогда коэффициент при xp в P не меньше 2, что невозможно.
Итак, на доске есть n финальных и 2n + 1 существенных многочленов, при этом не больше m из них являются и теми и другими. Значит, общее количество многочленов на доске не меньше чем n + (2n + 1) – m. С другой стороны, исходно на доске был n + 1 многочлен, а добавилось не больше чем mk. Значит, (n + 1) + mk ≥ n + (2n + 1) – m, или m(k + 1) ≥ 2n.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь