Олимпиадная задача по планиметрии для 10-11 класса от Емельянова Л. А.

Задача

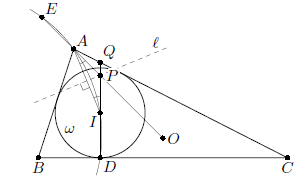
Окружность ω, вписанная в остроугольный неравнобедренный треугольник ABC, касается стороны BC в точке D. Пусть точка I – центр окружности ω, а O – центр описанной окружности треугольника ABC. Описанная окружность треугольника AID, пересекает вторично прямую AO в точке E. Докажите, что длина отрезка AE равна радиусу окружности ω.

Решение

Пусть для определенности AB < AC, а луч DI пересекает отрезки AO и AC в точках P и Q соответственно (см. рис).

Имеем: ∠AIP= ∠DQC– ∠IAC= 90° – ∠C– ½∠A и ∠IAP= ∠OAB–∠IAB= ½ (180° – ∠AOB) – ½∠A= 90° – ∠C– ½∠A. Таким образом, треугольникAPIравнобедренный (AP = PI), то есть точкаPлежит на серединном перпендикуляреlкAI, и лучиPAиPIсимметричны относительноl. Описанная окружность треугольникаAIDтакже симметрична относительноl. Следовательно, отрезкиAEиIDтоже симметричны, поэтому они равны.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии для 10-11 класса от Емельянова Л. А.

Задача

Решение

Ответ

Подтверждение удаления