Олимпиадная задача по планиметрии про треугольник ABC и вписанные окружности (сложность 3, 9-10 класс, А. Полянский)

  Обозначим через I центр окружности, вписанной в треугольник ABC, а через A₀, B₀, C₀ – точки её касания со сторонами BC, CA, AB, соответственно. Будем считать, что точка A₁ лежит на отрезке A₀B. Заметим, что  CA₀ + AC₀ = CB₀ + AB₀ = CA.  Из условия следует, что  CA₁ + AC₁ = CB₁ + AB₁ = CA.  Отсюда  CA₀ – CA₁ = AC₁ – AC₀;  это значит, что  A₁A₀ = C₁C₀,  и точка C₁ лежит на отрезке C₀A. Поэтому прямоугольные треугольники IA₀A₁ и IC₀C₁ равны по двум катетам (см. рис.).

  Далее можно рассуждать по разному.   Первый способ.  ∠IA₁C = ∠IC₁B,  следовательно, четырёхугольник BC₁IA₁ вписан. Точки B, I_B и I лежат на одной прямой (биссектрисе угла A₁BC₁), поэтому  ∠A₁I_BI = ∠BA₁I_B + ∠A₁BI_B = ∠I_BA₁C₁ + ∠C₁BI = ∠I_BA₁C₁ + ∠C₁A₁I = ∠I_BA₁I.  Значит, треугольник II_BA₁ равнобедренный:  II_B = IA₁. Аналогично  II_B = IC₁ = II_A = IB₁ = II_C = IA₁.  Следовательно, I – центр описанной окружности треугольника I_AI_BI_C.

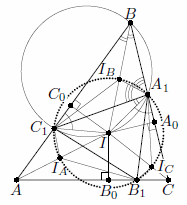
  ∠A₁IC₁ = ∠A₀IC₀ = 180° – ∠B.  Значит,  ∠A₁B₁A₁ = 90° – ½ ∠B = 180° – ∠A₁I_BC₁  (см. задачу 155448). Следовательно, точка I_B лежит на Ω.

  Так же доказывается, что на Ω лежат I_A и I_C.

Ответ задачи отсутствует