Олимпиадная задача по планиметрии: точки на окружности, 9

Задача

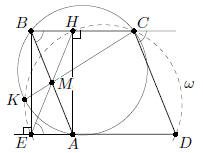
Дан параллелограмм ABCD с тупым углом A. Точка H – основание перпендикуляра, опущенного из точки A на BC. Продолжение медианы CM треугольника ABC пересекает описанную около него окружность в точке K. Докажите, что точки K, H, C и D лежат на одной окружности.

Решение

Пусть E – основание перпендикуляра, опущенного из точки B на AD. Тогда четырёхугольник AHBE – прямоугольник. Значит, ∠HED = ∠ABC = 180° – ∠BCD, то есть точки D, C, H, E лежат на некоторой окружности ω (см. рис.).

Заметим, чтоM– точка пересечения диагоналей прямоугольникаAHBE. Поскольку точкиA,K,B,Cлежат на одной окружности, MK·MC=MA·MB=MH·ME. Это равенство означает, что точкиC,K,HиEлежат на одной окружности. Эта окружность совпадает с ω, так как имеет с ней три общие точки. Итак, точкиK,H,C,Dлежат на ω.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: окружность и параллелограмм, 9-10 класс

Задача

Решение

Ответ

Подтверждение удаления