Олимпиадная задача по планиметрии: минимизация суммы расстояний до точек внутри окружности

  Пусть даны точки A и B. Тогда геометрическое место таких точек M, что  AM + BM = a (= const)  есть эллипс с фокусами A и B. Если точка K лежит внутри эллипса, то  AK + BK < a,  а если вне, то  AK + BK > a.

  Рассмотрим семейство эллипсов с фокусами A и B. Наибольший из этих эллипсов, лежащий внутри окружности, касается её либо в точке, лежащей на серединном перпендикуляре к AB (рис. слева), либо в двух точках, симметричных относительно этого перпендикуляра (рис. справа). Ясно, что искомый минимум суммы расстояний достигается в точках касания.

  Выясним, когда имеет место второй случай. ПустьM– одна из точек касания. В силуоптического свойства эллипса MO– биссектриса углаAMB. Тогда, поскольку  OA = OB  и  AM ≠ MB,  точкиA, M, BиOлежат на одной окружности. Отсюда получаем следующее построение.   Проведём окружность через точкиA, OиB. Если она пересекает данную окружность, то каждая из точек пересечения является искомой. Если же окружности не пересекаются, то искомой будет ближайшая кAточка пересечения данной окружности и серединного перпендикуляра кAB.

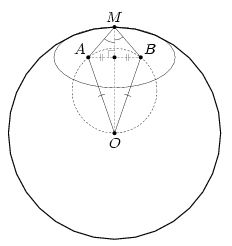
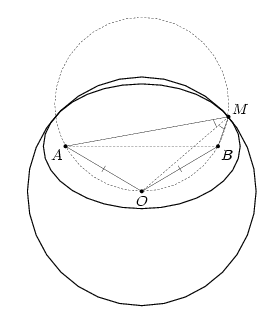
Ответ задачи отсутствует