Олимпиадная задача по планиметрии с углами и равными сторонами в пятиугольнике

Решение 1:   Пусть  AB = AE = a,  CB = CD = b,  ∠ABC = α.  Тогда 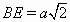  , 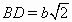  ,  ∠EBD = α – 90° (рис. слева).  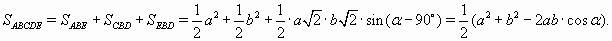   Но по теореме косинусов  a² + b² – 2ab cos α = AC² = 1.  То есть  S_ABCDE = 0,5.

                       

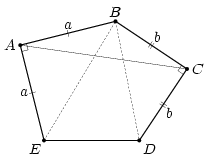
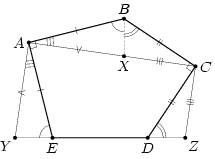
Решение 2:   ∠B + ∠E + ∠D = 360°.  Следовательно, на отрезке AC найдётся такая точка X, что углы ABX и CBX дополняют до 180° углы E и D соответственно (рис. в центре). Повернём треугольники ABX и CBX на –90° и 90° относительно вершин A и C соответственно. Пусть точки Y и Z – образы точки X при этих поворотах. Тогда YACZ – прямоугольная трапеция, в которой высота AC равна 1 и сумма оснований  AY + CZ = AC = 1.  Следовательно,

S_ABCD = S_YACZ = 0,5.

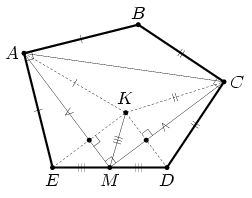
Решение 3:   Рассмотрим точку K, симметричную точке B относительно AC (рис. справа). Тогда треугольники KAE и KCD равнобедренные, и подсчёт углов показывает, что  ∠EKD = 90°. 

  Пусть M – середина стороны DE. Тогда  MK = ME,  и значит, треугольники AKM и AEM равны. По той же причине равны треугольники CKM и CDM. Поэтому  S_ABCDE = 2S_AMC. 

  ∠MAC = ½ ∠EAD = 45╟,  аналогично  ∠MCA = 45╟,  то есть треугольник AMC – прямоугольный равнобедренный с гипотенузой 1. Cледовательно,  S_AMC = 0,25,  а  S_ABCDE = 0,5.

0,5.