Задание олимпиады по планиметрии: центр вписанной окружности и треугольник средних линий

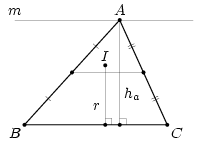
Пусть центр I вписанной окружности треугольника ABC не лежит внутри треугольника, образованного средними линиями. Тогда расстояние от I до одной из сторон не меньше, чем половина высоты, проведённой к этой стороне. Так как это расстояние является радиусом вписанной окружности, то диаметр этой окружности не меньше высоты. Но это невозможно, так как в этом случае вписанная окружность должна иметь общую точку с прямой m, параллельной этой стороне и проходящей через противолежащую вершину (см. рис.).

Верно.