Олимпиадная задача по планиметрии: восстановление треугольника по высотам, медиане и биссектрисе

  Пусть C₀ и C₁ – основания медианы и биссектрисы, проведённых из вершины C треугольника ABC, а H – его ортоцентр. Тогда точки P и Q, симметричные H относительно прямой AB (то есть прямой C₀C₁) и точки C₀, лежат на описанной окружности треугольника (см. задачи 155463 и 208949. Кроме того,  AQ = BH = BP,  то есть CC₁ – биссектриса угла PCQ.

  Первый этап во всех способах решения – построение точек P и Q (рис. слева).   Первый способ. 1) Построим окружность с центром C₁, касающуюся прямой PH, и проведём к ней касательную из точки Q. Эта касательная пересечёт прямую PH в вершине C (поскольку прямая PH проходит через точку C, а прямые CP и CQ симметричны относительно биссектрисы CC₁).

  2) Построим окружность, проходящую через точки C, P и Q, и найдем точки A и B её пересечения с прямой C₀C₁. Треугольник ABC искомый.

             

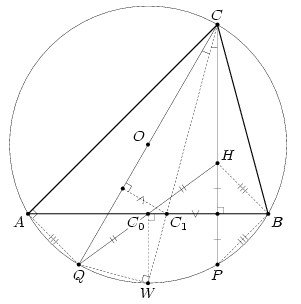
     а) середина W дуги AB лежит на пересечении серединного перпендикуляра к отрезку AB и биссектрисы CC₁ (рис. слева);

     б) поскольку PQ || AB, то CQ – диаметр описанной окружности, то есть  ∠CWQ = 90°.

  1) Построим точку W как пересечение окружности с диаметром C₁Q и перпендикуляра к C₀C₁, проведённого в точке C₀.

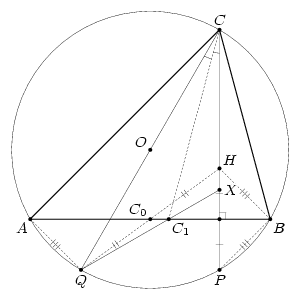
  2) Построим окружность, проходящую через точки W, P и Q. Найдём точки A и B её пересечения с прямой C₀C₁ и точку C её пересечения с прямой PH. Треугольник ABC искомый.   Третий способ. 1) Построим точку X пересечения прямых QC₁ и HP (рис. справа).

  2) Построим окружность Аполлония – ГМТ точек M, для которых  MQ : MX = C₁Q : C₁X.

  3) Построим точку C как пересечение этой окружности и прямой PH (в той же полуплоскости относительно C₀C₁, что и H).

  4) См. п. 2) первого способа.

Ответ задачи отсутствует