Олимпиадная задача по планиметрии для 8-9 класса от Блинкова Ю. А.
Задача
Дана окружность и хорда AB, отличная от диаметра. По большей дуге AB движется точка C. Окружность, проходящая через точки A, C и точку H пересечения высот треугольника ABC, повторно пересекает прямую BC в точке P. Докажите, что прямая PH проходит через фиксированную точку, не зависящую от положения точки C.
Решение
Решение 1: Поскольку точка C движется по большей дуге AB, то угол C – острый. Рассмотрим некоторое положение точки C, при котором треугольник ABC – остроугольный и точка P лежит на отрезке BC (см. рис.). Поскольку четырёхугольник ACPH – вписанный, то ∠PHA1 = ∠C. Рассмотрим окружность ΩC, симметричную описанной окружности треугольника ABC относительно AB. Как известно (см. задачу 155463), точка H принадлежит ΩC. Пусть X – точка пересечения ΩC и прямой PH. При движении точки C точка H двигается по окружности ΩC, но угол AHX, равный углу C, постоянен. Поэтому и точка X постоянна.
Случаи, когда точка P не лежит на отрезке BC или треугольник ABC – тупоугольный, рассматриваются аналогично (в случае тупоугольного треугольника ABC точка H движется по большей дуге окружности ΩC).
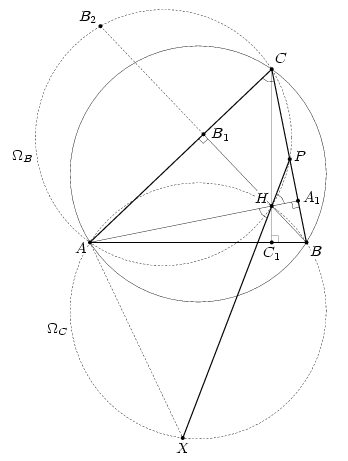
Решение 2: Наряду с упомянутой в условии окружностью ΩB рассмотрим окружность ΩC, проходящую через точки A, B и H (см. рис.). Обе они симметричны описанной окружности Ω треугольника ABC (см. задачу 155605). Значит, они симметричны друг другу относительно общей хорды AH. При этой симметрии прямая BC, перпендикулярная AH, переходит в себя, поэтому точка B переходит в точку P, а прямая PH – в прямую BH. Последняя прямая пересекает ΩB в точке B2, симметричной B относительно AC. Следовательно, точка X пересечения прямой PH с ΩC получается из фиксированной точки B композицией двух симметрий: сначала относительно AC, потом относительно AH, то есть поворотом вокруг точки A на удвоенный угол между прямыми AC и AH. Но угол между этими прямыми равен 90° – ∠C, то есть постоянен.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь