Олимпиадная задача по планиметрии: центр описанной окружности и перпендикулярность OI (8-9 класс)

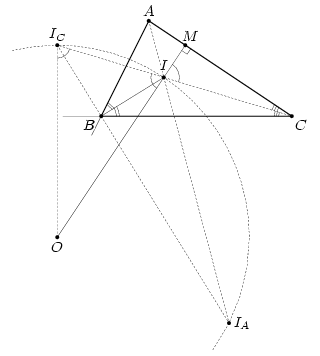
Решение 1:   Центры вневписанных окружностей I_A, I_C лежат на биссектрисе внешнего угла при вершине B (рис. слева). Пусть  ∠A = 2α,  ∠B = 2β,  ∠C = 2γ.  Нетрудно проверить, что  ∠ABI_A = 90° + β,  ∠BIA_A = 90° – α – β.  Поэтому  ∠I_COI = 2∠I_CI_AI = 180° – 2α – 2β = 2γ.

  Из равнобедренного треугольника I_COI получаем, что  ∠OII_C = 90° – γ.  Поскольку ∠CIM = ∠OII_C,  то в треугольнике IMC (M – точка пересечения прямых OI и AC)  ∠ICM + ∠CIM = γ + 90° – γ = 90°,  что и требовалось доказать.

             

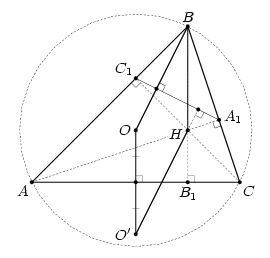
Решение 2:   Треугольник ABC, очевидно, является ортотреугольником треугольника I_AI_BI_C. Таким образом, задача сводится к следующему утверждению.   Пусть AA₁ и CC₁ – высоты остроугольного треугольника ABC, H – его ортоцентр, а O' – центр описанной окружности треугольника AHC. Тогда  O'H ⊥ A₁C₁.

  Докажем это. Пусть O – центр описанной окружности треугольника ABC. Как известно:

     1)   OB ⊥ A₁C₁ (см. задачу 152815);

     2)  O и O' симметричны относительно прямой AC (см. задачу 155605));

     3) Расстояние от точки O до прямой AC в два раза меньше длины отрезка BH (см. задачу 153528)).

   Из утверждений 2) и 3) следует, что OO'HB – параллелограмм (рис. справа). Теперь требуемое следует из 1).

Ответ задачи отсутствует