Олимпиадная задача по планиметрии для 8-9 класса: совпадение вершин многоугольников
Задача
На плоскости даны два равных многоугольника F и F'. Известно, что все вершины многоугольника F принадлежат F' (могут лежать внутри него или на границе). Верно ли, что все вершины этих многоугольников совпадают?
Решение
Контрпример: четырёхугольники ABCD и DBKA на рисунке (треугольник ABD – равносторонний, а точки K и C симметричны относительно его высоты BB').
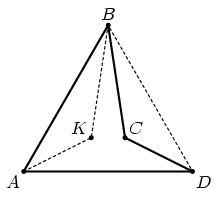
Ответ
Неверно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет