Олимпиадная задача по планиметрии: углы в равностороннем треугольнике с точками K, L, M
Задача
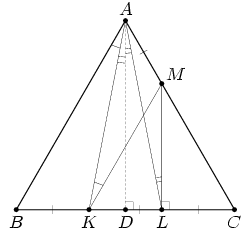
На стороне ВС равностороннего треугольника АВС отмечены точки K и L так, что BK = KL = LC, а на стороне АС отмечена точка М так,
что АМ = ⅓ AC. Найдите сумму углов AKM и ALM.
Решение
Решение 1: Заметим, что треугольник MKC – также равносторонний, так как CM = 2/3 CA = 2/3 CB = CK и ∠MCK = 60° (рис. слева). Следовательно, MK || AB, поэтому ∠АKМ = ∠KАВ.
Медиана ML треугольника MKC является его высотой и, значит, параллельна высоте AD треугольника АВС; поэтому ∠АLМ = ∠LАD.
D – середина KL, значит, треугольник KAL – равнобедренный; следовательно, его высота AD является и биссектрисой, то есть ∠LАD = ∠KАD.
Таким образом, ∠АKМ + ∠АLМ = ∠KАВ + ∠KАD = ∠BАD = 30°.
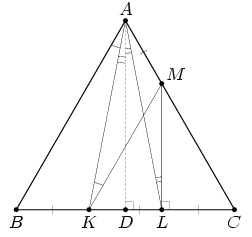
Решение 2: Пусть точка N симметрична M относительно высоты AD (рис. справа). Тогда ∠АKМ + ∠АLМ = ∠АLN + ∠АLМ = ∠NLM = ∠BLM – ∠BLN = 30° (треугольник BLN равносторонний; а ML ⊥ BC, как показано в решении 1).
Ответ
30°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь