Олимпиадная задача по планиметрии для 8-9 класса от Гордина Р. К.

Задача

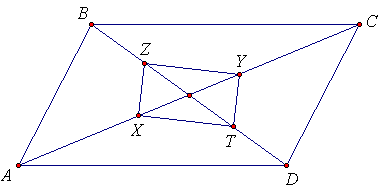
Дан параллелограмм ABCD. Вписанные окружности треугольников ABC и ADC касаются диагонали AC в точках X и Y. Вписанные окружности треугольников BCD и BAD касаются диагонали BD в точках Z и T. Докажите, что если все точки X, Y, Z, T различны, то они являются вершинами прямоугольника.

Решение

Четырёхугольник XZYT, как и вся картинка, симметричен относительно центра O параллелограмма ABCD (см. рис.).

Значит,XZYT– параллелограмм. Осталось проверить, что его диагонали равны. Пусть BC = a, AC = b, AB = c. По известным формулам для расстояния от вершин треугольника до точек касания сторон с вписанной окружностью (см. задачу152554) AX= ½ (b + c – a), AY = CX= ½ (a + b – c), поэтому XY = |AX – AY| = |c – a|, то есть разности сторон параллелограммаABCD. Ясно, что тот же результат мы получим и для отрезкаZT.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: точки касания окружностей в параллелограмме

Задача

Решение

Ответ

Подтверждение удаления