Олимпиадная задача по математике о делимости коэффициентов бинома Ньютона для 11 класса

  Пусть p – простое число и  n = n₀ + n₁p + n₀p² + ... + n_kp^k = (n_k...n₁n₀)_p  – p-ичное представление числа n. Покажем, что

S(n, p) = (n₀ + 1)(n₁ + 1)...(n_k + 1).   Первый способ. Будем рассматривать многочлены над полем вычетов Z_p по модулю p. Здесь  S(n, p)  равно количеству ненулевых коэффициентов многочлена  (x + 1)ⁿ.  Заметим, что биномиальный коэффициент 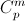    делится на p при  m = 1, ..., p – 1,  а  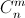   не делится на p при любом  n < p, m = 0, ..., n. .

  Отсюда сразу следует, что над Z_p   (x + 1)^p = x^p + 1,  (x + 1)^p² = (x^p + 1)^p = x^p² + 1,  ...,  (x + 1)^pm = x^pm + 1,  ...

  Поэтому   (x + 1)ⁿ = (x + 1)^n₀(x + 1)^n₁p...(x + 1)^n_kpk = (x + 1)^n₀(x^p + 1)^n₁...(x^pk + 1)^n_k.   Раскладывая  (x^pi + 1)^n_i  по биному, мы получаем многочлен от x^pi, все коэффициенты которого, как сказано выше, отличны от нуля. Этих коэффициентов ровно  n_i + 1.  Перемножив теперь все скобки мы получим сумму  (n₀ + 1)(n₁ + 1)...(n_k + 1)  одночленов вида x^m₀x^m₁p...x^m_kpk с ненулевыми коэффициентами. Поскольку  m_i ≤ n_i < p,  среди этих одночленов нет одинаковых, то есть "приведения подобных" не происходит и число  S(n, p)  ненулевых коэффициентов многочлена  (x + 1)ⁿ  равно

(n₀ + 1)(n₁ + 1)...(n_k + 1).   Второй способ. Надо подсчитать, сколько чисел среди 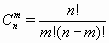  ,  m = 0, 1, ..., n  не делятся на p.   Степень простого числа p, на которую делится n!, равна  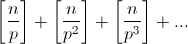   (см. задачу 160553). Поэтому степень p, на которую делится 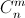,  равна   ...   Но  [a + b] ≥ [a] + [b]  для любых действительных чисел a и b. При этом  [a + b] = [a] + [b]  тогда и только тогда, когда  {a} + {b} < 1,  то есть

{a} ≤ {a + b}.  Получаем, что все слагаемые в выписанной выше сумме неотрицательны, и для того, чтобы 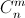     не делилось на p, надо, чтобы все они равнялись 0, а это равносильно тому, что  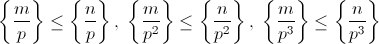   и т. д.

  Пусть  n = (n_k...n₁n₀)_p  и  m = (m_k...m₁m₀)_p  – p-ичные представления чисел n и m. Тогда требуемое условие равносильно тому, что  m₀ ≤ n₀,  m₁ ≤ n₁,

m₂ ≤ n₂  и т. д. Значит, m_i может принимать ровно  n_i + 1  значений. Всего вариантов для m:  (n₀ + 1)(n₁ + 1)...(n_k + 1).   Вернёмся к решению задачи.   а) Так как 3 – простое число, а  2012 = (2202112)₃,  то  S(2012,3) = 3⁴·2² = 324.   б) Число 2011 простое, а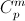  

  В этой сумме все слагаемые, начиная с четвёртого, делятся на 2011⁴, а первые три слагаемых дают  1 + 2011² + 1005·2011³.  Это означает, что в представлении числа 2012²⁰¹¹ в системе счисления с основанием 2011 младшие разряды такие:  n₀ = 1,  n₁ = 0,  n₂ = 1,  n₃ = 1005.  Поэтому

S(2012²⁰¹¹, 2011)  делится на  (n₀ + 1)(n₃ + 1) = 2012.

а) 324.