Олимпиадная задача Блинкова: футбольный турнир, текстовые задачи, индукция
Задача
а) В футбольном турнире в один круг участвовало 75 команд. За победу в матче команда получала 3 очка, за ничью 1 очко, за поражение 0 очков. Известно, что каждые две команды набрали различное количество очков. Найдите наименьшую возможную разность очков у команд, занявших первое и последнее места.б) Тот же вопрос для n команд.
Решение
б) Минимальный разрыв между первым и последним местом не может быть меньше n – 1. Докажем, что для n > 3 можно составить схему турнира так, чтобы получить разрыв n – 1 (если n = 2 или 3, то очевидно, минимальный разрыв будет составлять 3 очка).
По индукции будем строить таблицу для n команд, в которой результаты – все целые числа от n – 2 до 2n – 3.
База (n = 4). Пример таблицы турнира для четырёх команд:
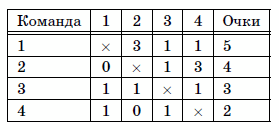
Ответ
а) 74; б) n – 1, если n > 3; 3, если n = 2 или 3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь