Олимпиадная задача по теории чисел для 7–9 классов от Богданова И. И.: доказать целостность 2x
Задача
Рациональные числа x, y и z таковы, что все числа x + y² + z², x² + y + z² и x² + y² + z целые. Докажите, что число 2x целое.
Решение
Приведём дроби x, y и z к виду с наименьшим общим знаменателем: x = a/D, y = b/D, z = c/D. Тогда НОД(a, b, c, D) = 1.
Число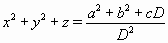 
целое, поэтому a² + b² делится на D. Аналогично на D делятся и суммы b² + c² и a² + c². Тогда и
2c² = (b² + c²) + (a² + c²) – (a² + b²) делится на D. Аналогично 2a² и 2b² делятся на D.
Если у D есть простой делитель p > 2, то a, b и c делятся на p, и НОД(a, b, c, D) ≥ p. Противоречие. Поэтому D – степень двойки.
Если D кратно 4, то a, b, c чётны, и мы опять получаем противоречие. Значит, D = 1 или D = 2. В частности, 2x = 2a/D – целое число.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь