Олимпиадная задача по планиметрии и комбинаторной геометрии: все ли отрезки пересекутся — задача 2/5, 7-9 класс, Шаповалов А. В.

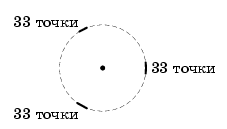
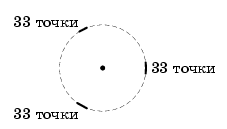
Есть несколько конфигураций точек, для которых Саша не сможет добиться своего. Приведём два примера.Конструкция 1. Поместим на окружности три маленькие дуги, полученные друг из друга поворотами на 120°, отметим по 33 точки на каждой дуге и ещё центр окружности (рис. слева). Отрезок из центра соединён с точкой на некоторой дуге. Он не пересечётся с отрезками, чьи концы лежат на других дугах. А такие отрезки есть, так как на двух дугах точек больше, чем на одной и в центре.

Конструкция 2. Возьмём квадрат ABCD и расположим 99 точек Q₁, ..., Q₉₉ на дуге BD окружности с центром A и радиусом, равным стороне квадрата. В качестве 100-й точки возьмём точку C (рис. справа). С какой бы точкой Q_n Саша ни соединил отрезком точку С, из оставшихся 49 отрезков Q_iQ_j отрезок CQ_n не будет пересекать вообще ни один: все отрезки Q_iQ_j лежат внутри круга с центром A и радиусом AB, а отрезок CQ_n – вне его.

Не всегда.