Олимпиадная задача по комбинаторной геометрии: план дворца шаха, 6×6, 5–7 классы
Задача
План дворца шаха – это квадрат размером 6×6, разбитый на комнаты размером 1×1. В середине каждой стены между комнатами есть дверь. Шах сказал своему архитектору: "Cломай часть стен так, чтобы все комнаты стали размером 2×1, новых дверей не появилось, а путь между любыми двумя комнатами проходил не более, чем через N дверей". Какое наименьшее значение N должен назвать шах, чтобы приказ можно было выполнить?
Решение
Рассмотрим произвольный маршрут из левого нижнего угла дворца в правый верхний. Так как надо "подняться" на 5 горизонталей и "сместиться вправо" на 5 вертикалей, то придётся пройти, как минимум, через 10 дверей, посетив при этом не меньше, чем 11 комнат (включая начальную и конечную).
11 комнат размером 1×1 не могли превратиться в 5 комнат размером 2×1. Следовательно, тот же маршрут в перестроенном дворце должен проходить, как минимум, через 6 комнат, а значит, не менее, чем через 5 дверей.
Такая перестройка дворца действительно возможна (см. рисунок).
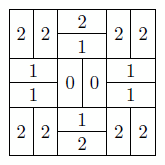
Ответ
N = 5.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь