Олимпиадная задача Петя и Вася: доказательство выигрыша в теории алгоритмов

  Предположим противное: у Васи есть стратегия, поволяющая ему гарантированно взять последний камень. Пусть d – изначальное количество камней, а r – остаток от деления d на n.  (r ≠ 0,  иначе Петя может сразу взять все камни).

  Петя после первого своего хода может, взяв кратное n количество камней, оставить любое количество вида  a_k = r + nk,  где  0 ≤ k ≤ n – 1  (все эти количества меньше n²). Пусть c_k – ответный ход в Васиной стратегии при a_k камнях в куче. Тогда c_k не делится на n, иначе после его хода остаётся 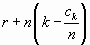    камней, и Петя может выиграть, действуя по Васиной стратегии для этого числа. Значит, все числа c_k меньше n, а тогда два из этих чисел совпадают. Пусть  c_k = c_l  (0 ≤ k < l ≤ n – 1).

  Напомним, что у Васи есть стратегия выигрыша в ситуации, когда в куче  a_k – c_k  камней и ход Пети.

  Пусть теперь Петя первым ходом оставит a_l камней; Вася в ответ возьмёт c_l камней. Теперь Петя может взять n(l – k) камней, оставляя  a_k – c_k,  и дальше действовать по вышеупомянутой Васиной стратегии. Таким образом, он выиграет. Противоречие.

Ответ задачи отсутствует