Олимпиадная задача о 10 автомобилях и флажках: комбинаторная геометрия 10–11 класс

  Введём в пространстве систему координат Oxyt. Обозначим через M точку шоссе, в которой в начальный момент находится первый автомобиль. Каждой точке шоссе A сопоставим точку  T_A(x_A, y_A) на плоскости Oxy,  где x_A – суммарная длина участков пути AM в населённых пунктах, а y_A – вне населённых пунктов. Тогда шоссе изображается некоторой ломаной на этой плоскости.

  Для i-й машины нарисуем график её движения, состоящий из всех точек  X_iA = (x_A, y_A, t_iA),  где t_iA – момент времени, в который эта машина находилась в точке A. Если эта машина была в точке M в момент t_i, а её скорости в населённых пунктах и вне их равны u_i и v_i, то 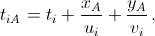    и, следовательно, весь график движения i-й машины лежит в плоскости  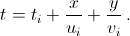   Обозначим эту плоскость через α_i.

  Рассмотрим теперь порядок, в котором машины проедут мимо некоторого флажкаF. Он совпадает с порядком, в котором плоскости α_iбудут пересекать прямую, параллельнуюOtи проходящую через точкуT_F. Пусть для двух флажковFиGэтот порядок различается (скажем, первая и вторая машины проехали мимо него в разном порядке). Тогда отрезкиX_1FX_1GиX_2FX_2Gпересекаются. Таким образом, если спроецировать прямую пересечения плоскостей α₁и α₂на плоскостьOxy, то точкиT_FиT_Gбудут лежать по разные стороны от полученной проекцииl₁₂.   Рассмотрим все прямыеl_ij. 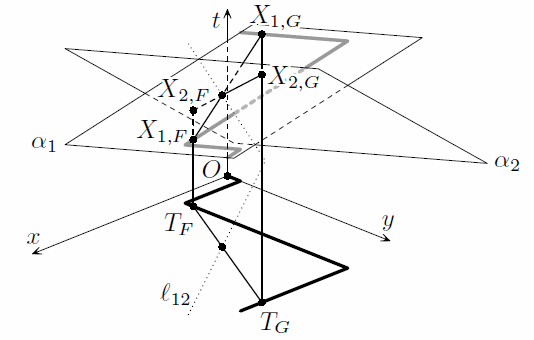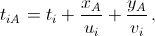Поскольку их количество не больше  ,   они разобьют плоскость не более чем на  45·46 : 2 + 1  частей (см. задачу160323). Значит, найдутся такие флажкиFиG, что точкиT_FиT_Gпопадают в одну часть, то есть ни одна проекция прямых их не разделяет. Поэтому на этих флажках порядок машин будет одинаков.

Ответ задачи отсутствует