Олимпиадная задача по планиметрии: ортоцентр треугольника центров описанных окружностей параллелограмма

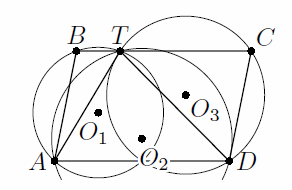
Решение 1:   Прямые O₁O₂ и O₃O₂ – серединные перпендикуляры к отрезкам AT и DT. Значит,  ∠AO₁O₂ = ∠TO₁O₂ = ∠TBA  (поскольку угол TO₁A – центральный для описанной окружности треугольника ABT). Аналогично  ∠DO₃O₂ = ∠TCD.  Отсюда  ∠TO₁O₂ + ∠TO₃O₂ = 180°.  Итак, точки T, O₁, O₂, O₃ лежат на одной окружности ω (рис. слева).

  Треугольники O₁TO₁ и O₁AO₂ симметричны относительно прямой O₁O₂. Значит, описанная окружность α треугольника AO₁O₂ равна ω. Аналогично описанная окружность δ треугольника DO₂O₃ также равна ω.

  Как известно (см. задачу 178187), ортоцентр H треугольника O₁O₂O₃ лежит на окружностях α и δ, то есть является второй точкой их пересечения. Пусть H' – вторая точка пересечения α с прямой AD. Тогда  ∠AH'O₂ = 180° – ∠AO₁O₂ = ∠DO₃O₂,  поэтому H' лежит на δ.

Значит, H' совпадает с H.

             

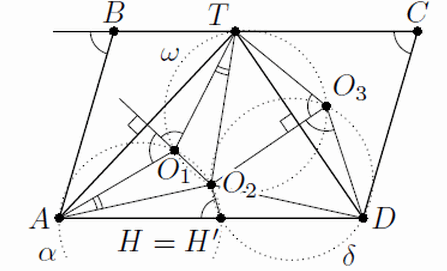
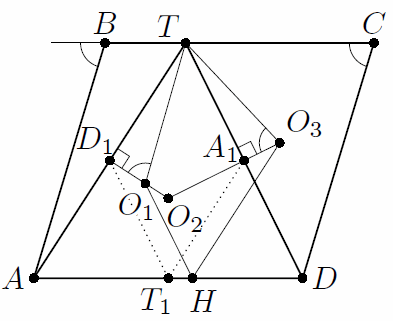
Решение 2:   Высоты треугольника O₁O₂O₃, опущенные из вершин O₁ и O₃, параллельны соответственно прямым DT и AT. Пусть H – точка пересечения первой из этих высот со стороной AD (рис. справа). Наша задача – показать, что  O₃H || AT.

  Обозначим через A₁, D₁ и T₁ середины сторон DT, AT и AD треугольника ADT, а через α, δ, τ – его углы при вершинах A, D, T соответственно. Тогда  ∠TO₁D₁ = 180° – ∠ABC = ∠BCD = ∠TO₃A₁.  Значит, прямоугольные треугольники TO₁D₁ и TO₃A₁ подобны, и    .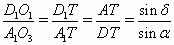

  Поскольку  O₁H || D₁T₁,  расстояния от точек O₁ и H до прямой D₁T₁ равны, то есть 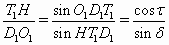   .   Отсюда

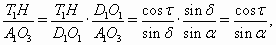     или 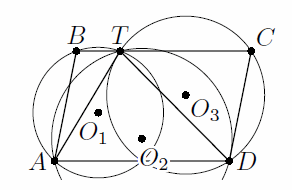  .   Это означает, что O₃ и H равноудалены от A₁T₁, то есть  O₃H || A₁T₁.

Ответ задачи отсутствует