Олимпиадная задача по многочленам и теории чисел для 8-10 класса от Сендерова В. А.
Задача
Для натуральных чисел a > b > 1 определим последовательность x1, x2, ... формулой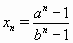 
. Найдите наименьшее d, при котором ни при каких a и b эта последовательность не содержит d последовательных членов, являющихся простыми числами.
Решение
При a = 4, b = 2 имеем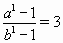 
, 
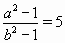. Осталось показать, что больше двух простых чисел подряд не встретится.
Докажем более сильное утверждение: при n > 2 хотя бы одно из чисел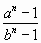 
, 
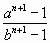не является простым. Предположим противное; тогда
(a – 1)(an–1 + ... + a + 1) = p(b – 1)(bn–1 + ... + b + 1), (1)
(a – 1)(an + ... + a + 1) = q(b – 1)(bn + ... + b + 1), (2)
где p и q – простые числа.
Пусть a – 1 не делится на b – 1. Тогда некоторое простое число r входит в разложение числа b – 1 в степени большей, чем в a – 1.
Из (1) и (2) следует, что r – общий делитель чисел an–1 + ... + a + 1 и an + ... + a + 1, но (an–1 + ... + a + 1, an + ... + a + 1) = (an–1 + ... + a + 1, an) = 1. Противоречие.
Пусть число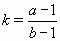 
целое. Тогда k(an–1 + ... + a + 1) = p(bn–1 + ... + b + 1), причём 1 < k < p, так как b < a. Значит, (k, p) = 1, поэтому
bn–1 + ... + b + 1 делится на k. Аналогично bn + ... + b + 1 делится на k. Но числа bn–1 + ... + b + 1 и bn + ... + b + 1, очевидно, взаимно просты. Противоречие.
Ответ
d = 3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь