Олимпиадная задача по планиметрии: равенство периметров в треугольнике для 8-10 классов
Задача
Пусть ABC – правильный треугольник. На его стороне AC выбрана точка T, а на дугах AB и BC его описанной окружности выбраны точки M и N соответственно так, что MT || BC и NT || AB. Отрезки AN и MT пересекаются в точке X, а отрезки CM и NT – в точке Y. Докажите, что периметры многоугольников AXYC и XMBNY равны.
Решение
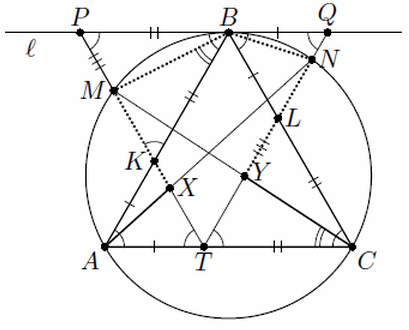
Решение 1: Пусть l – касательная к описанной окружности в точке B, а P и Q – точки пересечения l с лучами TM и TN соответственно. Обозначим через K и L соответственно точки, в которых лучи TM и TN пересекают стороны треугольника (см. рис. слева).
Четырёхугольники ABQT и BCTP – параллелограммы, откуда AT = BQ, CT = BP. Из параллельности имеем ∠KPB = ∠PBK = ∠LTC = 60°, то есть треугольники BPK и CLT – равносторонние. Поскольку BP = CT, эти треугольники равны. Из вписанности имеем
∠KBM = ∠ABM = ∠ACM = ∠TCY; значит, точки M и Y – соответственные в этих треугольниках, откуда BM = CY и PM = LY. Аналогично BN = AX и QN = KX. Кроме того, QL = BQ = AT, KP = BP = CT. Поэтому
XM + YN = KX + KM + LY + LN = QN + KM + PM + LN = QL + KP = AT + CT = AC.
Итак, PXMBNY = (XM + YN) + BM + BN + XY = AC + CY + AX + XY = PAXYC.
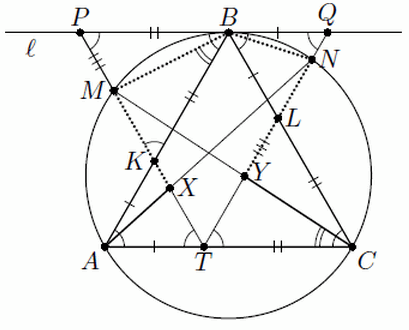
Решение 2: ∠AMY = ∠ABC = 60°. Тогда ∠AMY + ∠ATY = 180°, значит, точки A, M, Y, T лежат на одной окружности (см. рис. справа). Поэтому
∠MAY = ∠MTY = 60°, значит, треугольник MAY – правильный (два из его углов равны по 60°), T – точка на дуге AY его описанной окружности. Как известно (см. задачу 152355), TA + TY = ТM = TX + XM. Аналогично TС + TX = ТY + YN. Складывая эти два равенства, получаем AC = MX + NY.
Кроме того, MA + MB = = MC = MY + YC; поскольку MA = MY, получаем CY = MB. Аналогично AX = NB.
Итак, PAXYC = AC + AX + CY + XY = (MX + NY) + BN + BM + XY = PXMBNY.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь