Назад

Олимпиадная задача по планиметрии: отношение площадей в треугольнике, 9–11 класс

Задача 216622 • Сложность: 2 • 9-11 класс
Задача

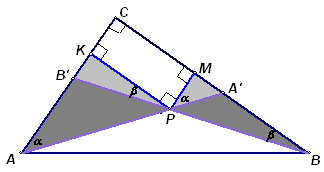
Внутри прямоугольного треугольника АВС выбрана произвольная точка Р, из которой опущены перпендикуляры PK и РМ на катеты АС и ВС соответственно. Прямые АР и ВР пересекают катеты в точках A' и B' соответственно. Известно, что  SAPB' : SKPB' = m.  Найдите  SMPA' : SBPA'.

Авторы:
Фольклор
Разделы:
Планиметрия
Источники:
Московская математическая регата Олимпиады и турниры 2011/12 10 класс
Количество версий:
5
Решение

SKPB' : SAPB' = KB' : AB',   SMPA' : SBPA' = MA' : BA'.  Докажем, что эти отношения равны. Для этого достаточно доказать, что  KB' : KA = MA' : MB.

Пусть  ∠KAP= ∠MPA'= α,  ∠MBP= ∠KPB'= β,  тогда  KB' = KPtg β =KAtg α tg β.  Аналогично и  MA'=MBtg α tg β.  Таким образом, оба отношения равны  tg α tg β.
Ответ

1/m.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет