Олимпиадная задача по планиметрии для 9-11 класса: площадь трапеции ABCD
Задача
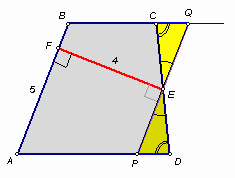
В трапеции ABCD (AD || BC) из точки Е – середины CD провели перпендикуляр EF к прямой AB. Найдите площадь трапеции, если АВ = 5, EF = 4.
Решение
Достаточно доказать, что площадь трапеции в два раза больше площади треугольника ABE (которая равна 10). Первый способ. Проведём через точку Е прямую, параллельную боковой стороне АВ, и отметим точки P и Q её пересечения с прямыми AD и ВС соответственно (см. рис.).
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет