Олимпиадная задача: максимальное число по пути в квадрате 3×3 для 6–7 класса
Задача
Квадрат 3×3 заполнен цифрами так, как показано на рисунке слева. Разрешается ходить по клеткам этого квадрата, переходя из клетки в соседнюю (по стороне), но ни в какую клетку не разрешается попадать дважды.
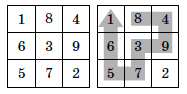
Решение
Если обойти все клетки доски, то получится девятизначное число, которое, конечно, будет больше любого восьмизначного.
Девятизначное число тем больше, чем больше его первая цифра. Но девятизначного числа, начинающегося с 9, построить не удастся. Более того, ни для какой из чёрных клеток (см. рисунок ниже) не существует начинающегося в ней пути, проходящего по всем клеткам доски. Действительно, ход из чёрной клетки всегда приводит в белую. Всего чёрных клеток четыре, поэтому белых клеток на любом таком пути тоже не более четырёх – все пять белых клеток так не обойти.

Ответ
Наибольшее число, которое можно получить, – 573618492 (см. рис.). 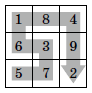
Чтобы оставлять комментарии, войдите или зарегистрируйтесь