Олимпиадная задача по планиметрии для 8–10 классов: равнодлинные векторы на плоскости
Задача
На плоскости нарисованы n > 2 различных векторов a1, a2, ..., an с равными длинами. Оказалось, что все векторы –a1 + a2 + ... + an,
a1 – a2 + a3 + ... + an, a1 + a2 + ... + an–1 – an также имеют равные длины. Докажите, что a1 + a2 + ... + an = 0.
Решение
Отложим векторы 2a1, ..., 2an из одной точки: пусть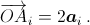 
Тогда все точки A1, ..., An различны и лежат на окружности ω с центром O. Пусть s = a1 + ... + an. По условию, все векторы s – 2ai имеют одну и ту же длину r. Рассмотрим такую точку S, что 
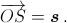Поскольку 
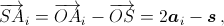все точки A1, ..., An лежат на окружности Ω с центром S и радиусом r.
Итак, окружности ω и Ω имеют n > 2 общих точек. Это значит, что они совпадают, а тогда и их центры совпадают, то есть s = 0.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь