Олимпиадная задача по числовым последовательностям для 8–10 класса от Мурашкина
Задача
Последовательность чисел a1, a2, ... задана условиями a1 = 1, a2 = 143 и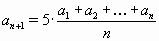 
при всех n ≥ 2.
Докажите, что все члены последовательности – целые числа.
Решение
Решение 1:Число a3 = 5·72 = 360 целое. При n ≥ 4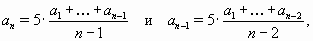 
откуда 
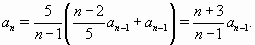Значит, если n≥ 4, то
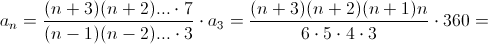(n+ 3)(n+ 2)(n+ 1)n.
Решение 2:Положим Sn =
a1 + a2 + ... + an,
тогда an+1 = Sn+1 – Sn. Достаточно показать, что все числа Sn – целые. Заметим, что S1 = 1, S2 = 144, и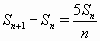 
, то есть 
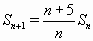. Значит, при n ≥ 2
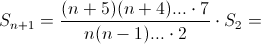
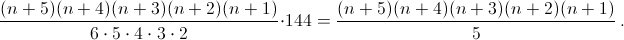
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет