Олимпиадная задача по планиметрии для 8-10 классов: доказательство параллельности прямых в выпуклом шестиугольнике
Задача
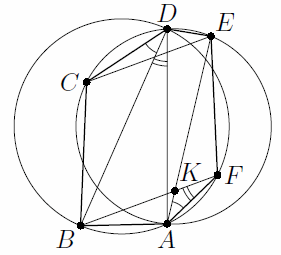
Дан выпуклый шестиугольник ABCDEF. Известно, что ∠FAE = ∠BDC, а четырёхугольники ABDF и ACDE являются вписанными.
Докажите, что прямые BF и CE параллельны.
Решение
Пусть K – точка пересечения отрезков AE и BF. ∠AKB = ∠AFB + ∠FAE = ∠ADB + ∠BDC = ∠ADC = ∠AEC. Это и значит, что BF || CE.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет