Олимпиадная задача по планиметрии и стереометрии для 8-10 класса от Емельяновой Т.

Решение 1:   Пусть B₀ – точка касания вписанной окружности со стороной AC. Точки A₀ и C₀ симметричны точке B₀ относительно биссектрис углов C и A соответственно. Можно считать, что точка D лежит на отрезке AB₀. Тогда точка E лежит на отрезке AC₀, а точка F – на продолжении отрезка CA₀, и

EC₀ = DB₀ = FA₀.

  Обозначим через M точку пересечения прямых EF и A₀C₀ (она лежит на отрезке EF). Отметим на прямой A₀C₀ точку G так, чтобы отрезки FG и AB были параллельны. Тогда треугольник GFA₀ подобен равнобедренному треугольнику C₀BA₀, значит,  FG = FA₀ = EC₀.  Из параллельности имеем

∠FEC₀ = ∠EFG  и  ∠EC₀G = ∠FGC₀.  Поэтому треугольники EC₀M и FGM равны по стороне и двум углам, и  EM = MF.

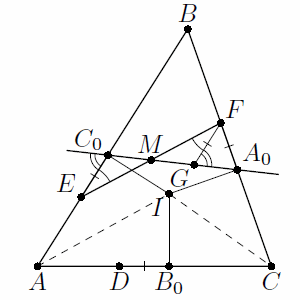
Решение 2:   Пусть I – центр вписанной окружности, M – точка пересечения прямых EF и A₀C₀. Прямоугольные треугольники IC₀E и IA₀F равны по двум катетам. Поэтому  ∠EIC₀ = ∠FIA₀,  значит, углы EIF и C₀IA₀ при вершинах равнобедренных треугольников EIF и C₀IA₀ равны. Следовательно, равны и углы IEF и IC₀A₀ при их основаниях, то есть точки I, C₀, E и M лежат на одной окружности. Поскольку угол IC₀E прямой, то и угол IME прямой, то есть IM – высота, а значит, и медиана равнобедренного треугольника EIF.

Решение 3:Пусть точка D движется с постоянной (равной 1) скоростью от A к C. Тогда точка E движется с той же скоростью от A к B, а F – с той же скоростью по прямой BC (в направлении 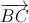  ).  При этом середина K отрезка EF движется с постоянной скоростью, равной полусумме единичных векторов, коллинеарных  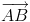  и 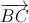  ,   (см. решение 2 задачи 156471), то есть параллельно биссектрисе внешнего угла B. Эта биссектриса параллельна основанию равнобедренного треугольника A₀BC₀. В момент, когда D совпадёт с B₀, точки E и F совпадут с точками C₀ и A₀, а точка K₀ – с серединой отрезка A₀C₀. Значит, точка K движется по прямой A₀C₀.

Ответ задачи отсутствует