Олимпиадная задача по стереометрии: развёртка многогранника в треугольник (10–11 класс)
Задача
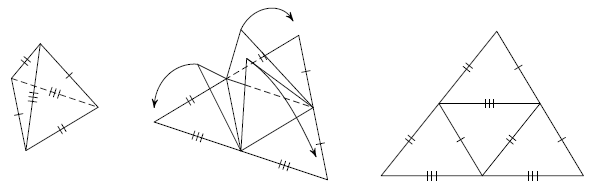
Известно, что всякую треугольную пирамиду, противоположные рёбра которой попарно равны, можно так разрезать вдоль трёх её рёбер и развернуть, чтобы её развёрткой стал треугольник без внутренних разрезов (см. рис.).
Решение
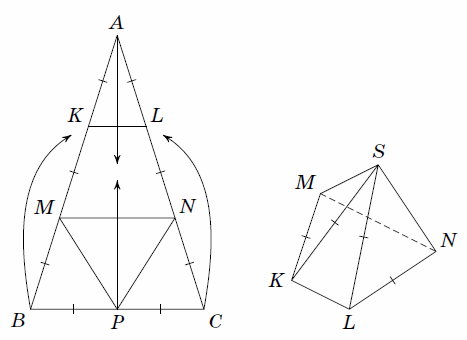
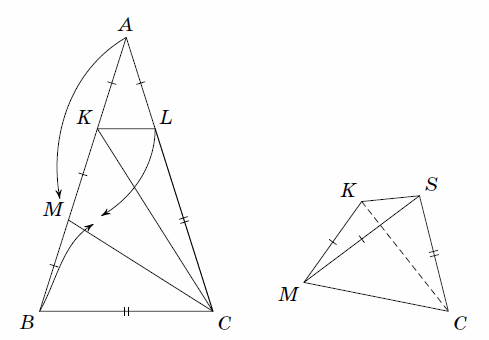
Подходящие выпуклые многогранники можно свернуть, например, из треугольника ABC со сторонами AB = AC = 3 и BC = 2. Разделим стороны на отрезки длины 1: BM = MK = KA = CN = NL = LA = BP = PC = 1 (рис. слева).
Ответ
Найдётся.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет