Олимпиадная задача о касательных и 2011-угольнике для 10–11 класса (Агаханов Н. Х.)

  Обозначим полученный правильный 2011-угольник через M, его вершины (по часовой стрелке) – через  X₁, X₂, ..., X₂₀₁₁,  его вписанную окружность через ω, а его центр – через O. Назовём прямые, содержащие стороны многоугольника, выделенными.

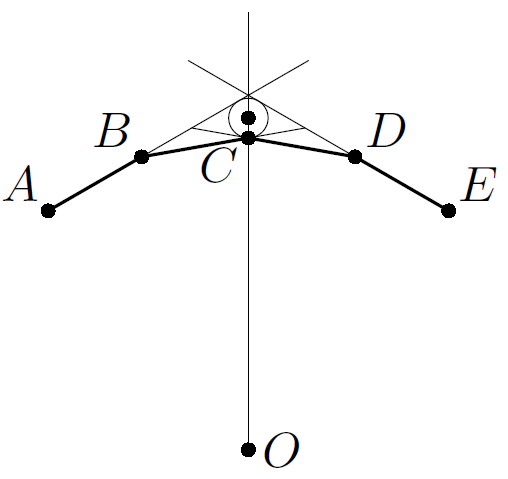
  Заметим, что для любых пяти последовательных вершин A, B, C, D, E многоугольника M существует окружность, отличная от ω, касающаяся прямых AB, BC, CD и DE.

  Действительно, вершиныAиE, а такжеBиDсимметричны относительно прямойCO. Тогда точка пересечения внешней биссектрисы углаABCс прямойCOотлична отOи равноудалена от прямыхAB, BC, CDиDE, а значит, является центром искомой окружности.   Если Вася нарисует 503 такие окружности для точек  (X₁,X₂,X₃,X₄,X₅),  (X₅,X₆,X₇,X₈, X₉),  ...,  (X₂₀₀₉,X₂₀₁₀,X₂₀₁₁,X₁,X₂),  а также окружность ω, то любая выделенная прямая будет общей касательной к двум проведённым окружностям. Итак, 504 окружностей достаточно.   Осталось доказать, что окружностей должно быть не менее 504. Каждой выделенной прямой должны касаться хотя бы две окружности. Окружность ω касается всех 2011 этих прямых. У каждой другой окружности есть не более четырёх общих касательных с ω, значит, она касается не более четырёх выделенных прямых. Итак, если окружностейn, то всего происходит не более чем  2011 + 4(n– 1)  касаний окружности с выделенными прямыми; с другой стороны, их должно быть не меньше  2011·2 = 4022.  Итак,  2011 + 4(n– 1) ≥ 2·2011,  откуда  n≥ 2011 : 4 + 1 > 503.

504 окружности.