Олимпиадная задача по планиметрии для 10-11 классов: равенство BP и CP в окружности
Задача
Остроугольный треугольник ABC вписан в окружность ω. Касательные к ω, проведённые через точки B и C, пересекают касательную к ω, проведённую через точку A, в точках K и L соответственно. Прямая, проведённая через K параллельно AB, пересекается с прямой, проведённой через L параллельно AC, в точке P. Докажите, что BP = CP.
Решение
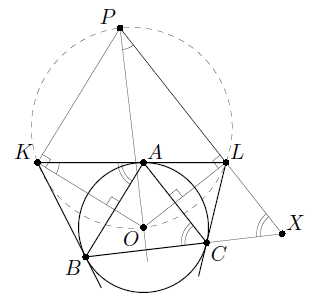
Решение 1:Пусть O – центр окружности w, а X – точка пересечения прямых BC и PL. Точки A и B симметричны относительно прямой OK, поэтому
OK ⊥ AB || KP. Аналогично OL ⊥ LP. Значит, K и L лежат на окружности с диаметром OP, и ∠OPL = ∠OKL. Из касания вытекает, что
∠KAB = ∠ACB = ∠PXB. Таким образом, ∠OPX + ∠PXB = ∠OKL + ∠KAB = 90°, то есть точка P лежит на серединном перпендикуляре к отрезку BC.
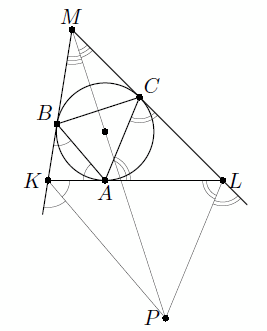
Решение 2:Пусть прямые BK и CL пересекаются в точке M. Прямая KP, параллельная основанию равнобедренного треугольника ABK, является биссектрисой внешнего угла при вершине K. Аналогично LP – биссектриса внешнего угла при вершине L. Следовательно, P – центр вневписанной окружности треугольника KLM, касающейся стороны KL и поэтому лежит на биссектрисе угла M. Поскольку MB = MC, точки B и C симметричны относительно этой биссектрисы. Значит, и отрезки PB и PC также симметричны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь