Олимпиадная задача по планиметрии: Ромб OPHQ и коллинеарность точек в треугольнике ABC

Решение 1:   Пусть BB' и CC' – высоты треугольника. Так как OB₀ и OC₀ – серединные перпендикуляры к сторонам AC и AB, то отрезки B'B₀ и C'C₀ равны высотам ромба OPHQ. Значит,  B'B₀ = C'C₀.  Но эти отрезки являются проекциями отрезка OH на прямые AB и AC, поэтому, OH составляет равные углы с этими прямыми. Это означает, что прямая OH параллельна либо внутренней, либо внешней биссектрисе угла BAC.

  Так как  ∠AOC = 2∠B,  то  ∠CAO = 90° – ∠B = ∠BAH.  Это значит, что лучи AO и AH симметричны относительно биссектрисы l угла A. Поэтому OH пересекает l и не может быть ей параллельна. Итак, l перпендикулярна OH, то есть является биссектрисой и высотой треугольника AOH. Отсюда

AH = AO,  и точка A, как и точки P, Q, лежит на серединном перпендикуляре к отрезку OH.

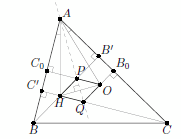
Решение 2:   Положим  a = BC,  b = CA,  c = AB,  α = ∠A;  тогда  AB' = c cos α,  AC' = b cos α.  Как и выше,  B'B₀ = C'C₀,  откуда  |AB₀ – AB'| = |AC₀ – AC'|,  или

|b – 2c cos α| = |c – 2b cos α|.

  Рассмотрим два случая.

  1)  b – 2c cos α = c – 2b cos α.  Тогда  (b – c)(1 + 2 cos α) = 0.  По условию cosα > 0 и, значит, b = c, что противоречит условию.

  2)  b – 2c cos α > 0,  c – 2b cos α < 0  (геометрически это означает, что точка B' лежит между A и B₀, а точка C₀ – между A и C', см. рис.). Тогда

b – 2c cos α = 2b cos α – c,  или  (b + c)(1 – 2 cos α) = 0.  Таким образом,  α = 60°,  AC' = b cos α = AB₀.  Значит, точки B₀ и C' симметричны относительно биссектрисы l угла A. Тогда прямые OB₀ и CC' также симметричны, и их точка пересечения Q лежит на l. Аналогично точка P лежит на l.

Ответ задачи отсутствует