Задание олимпиады по математике: сколько n не превосходящих 2012 сумма степеней оканчивается на 0
Задача
Сколько существует таких натуральных n, не превосходящих 2012, что сумма 1n + 2n + 3n + 4n оканчивается на 0?
Решение
Решение 1: Разберём три случая.
1) n нечётно. Тогда число 1n + 4n нечётно и делится на 1 + 4 = 5. Следовательно, оно оканчивается на 5. Аналогично на 5 оканчивается число БикЮ 2n + 3n. Значит, данная сумма оканчивается на 0.
2) n = 4k + 2. Тогда число 1n + 2n нечётно и делится на 1² + 2² = 5. Следовательно, оно оканчивается на 5. Число 3n + 4n также нечётно и делится на 3² + 4² = 25. Снова наша сумма оканчивается на 0.
3) n = 4k. Последняя цифра чисел 24 и 44 равна 6. Значит, и последняя цифра чисел 2n = (24)k и 4n = (44)k равна 6. Аналогично последняя цифра числа 3n равна 1. Следовательно, наша сумма оканчивается на 4.
Среди 2012 последовательных чисел чисел, кратных 4, ровно четверть, то есть 503. А "хороших" чисел 2012 – 503 = 1509.
Решение 2: Составим таблицу значений последних цифр у каждого слагаемого и у суммы для нескольких начальных значений n.
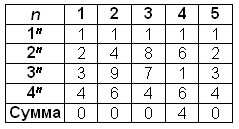
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь