Олимпиадная задача по планиметрии: угол IMA в треугольнике с вписанной окружностью

Решение 1:   Пусть r – радиус окружности, вписанной в треугольник АВС, D, E и F – точки её касания со сторонами АВ, ВС и АС соответственно (см. рис.).

  Очевидно четырёхугольник CEIF– квадрат, поэтому  CE = r.   По условию  АВ= 2АC,  значит,  АM = AC.  Отсюда  DM = AM – AD = AC – AF = r.   Таким образом, треугольникIDM– прямоугольный и равнобедренный, следовательно,  ∠IMA= 45°.   Замечание. Равенство  DМ = r  можно также получить из формулы для вычисления радиуса вписанной окружности в прямоугольном треугольнике (см. задачу 152552) и равенства  BD = p – b  (см. задачу 152554).

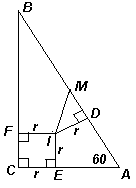
Решение 2:   Рассмотрим равносторонний треугольник АВD, для которого отрезок ВС служит медианой. При симметрии относительно биссектрисы угла А середина M стороны АВ переходит в середину C стороны АD. Следовательно, угол IMА равен углу IСA, который, очевидно. равен 45°.

45°.