Олимпиадная задача по стереометрии для 10-11 класса: расстояния в кубе
Задача
В кубе ABCDA1B1C1D1, ребро которого равно 6, точки M и N – середины рёбер AB и B1C1 соответственно, а точка K расположена на ребре DC так, что
DK = 2KC. Найдите
а) расстояние от точки N до прямой AK;
б) расстояние между прямыми MN и AK;
в) расстояние от точки A1 до плоскости треугольника MNK.
Решение
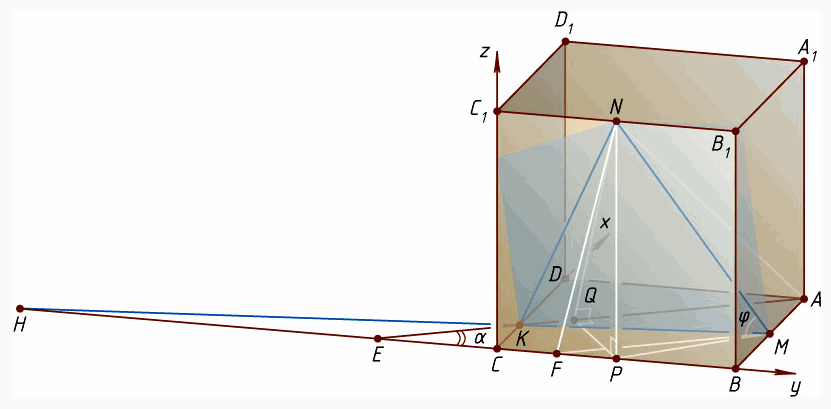
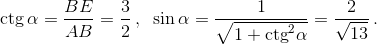 Из прямоугольного треугольникаPQEнаходим, что
Из прямоугольного треугольникаPQEнаходим, что 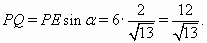 Следовательно,
Следовательно, 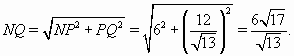 б) Через точкуMпроведём прямую, параллельнуюAK. Пусть
эта прямая пересекаетBCв точкеF. Тогда угол между прямымиMNиAKравен углу между прямымиMNиMF. Из прямоугольного треугольникаMBFнаходим, что
б) Через точкуMпроведём прямую, параллельнуюAK. Пусть
эта прямая пересекаетBCв точкеF. Тогда угол между прямымиMNиAKравен углу между прямымиMNиMF. Из прямоугольного треугольникаMBFнаходим, что 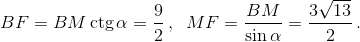 Значит,
Значит, 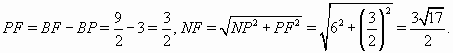 Кроме того,
Кроме того, 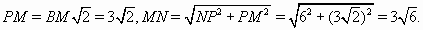 Рассмотрим треугольникMNF. Обозначим ∠NMF= φ. По теореме косинусов
Рассмотрим треугольникMNF. Обозначим ∠NMF= φ. По теореме косинусов 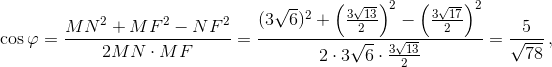 ,
, 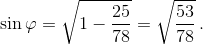 Из прямоугольного треугольникаADKнаходим, что AK² =AD² +DK² = 36 + 16 = 52.
ПустьV– объём тетраэдраAKMN. Тогда, с одной стороны V= ⅓SAKM·NP= ⅓·½AM·AD·NP= ⅓·½·3·6·6 = 18, с другой стороны, еслиd– искомое расстояние между прямымиAKиMN, то
Из прямоугольного треугольникаADKнаходим, что AK² =AD² +DK² = 36 + 16 = 52.
ПустьV– объём тетраэдраAKMN. Тогда, с одной стороны V= ⅓SAKM·NP= ⅓·½AM·AD·NP= ⅓·½·3·6·6 = 18, с другой стороны, еслиd– искомое расстояние между прямымиAKиMN, то 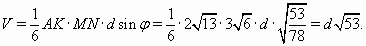 Из уравнения
Из уравнения 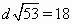 находимd. в) Продолжим отрезок MK до пересечения с прямой BC в точке H. Из подобия треугольников KCH и MBH находим, что
находимd. в) Продолжим отрезок MK до пересечения с прямой BC в точке H. Из подобия треугольников KCH и MBH находим, что 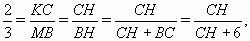 откуда CH = 12.
откуда CH = 12.
Выберем прямоугольную систему координат, приняв за начало точку C, направив ось CX по лучу CD, ось CY – по лучу CB, а ось CZ – по лучу CC1. Найдём координаты нужных нам точек: C(0, 0, 0), K(2, 0, 0), A(6, 6, 6), H(0, –12, 0), N(0, 3, 6). Уравнение плоскости MNK имеет вид
x/2 – y/12 + z/c = 1 (уравнение плоскости в отрезках), где (0, 0, c) – координаты точки пересечения плоскости MNK с осью CZ. Подставив в это уравнение координаты точки N, найдём, что c = 24/5. Значит, уравнение плоскости ABC – 12x – 2y + 5z – 24 = 0.
Искомое расстояние от точки A1 до плоскости MNK равно 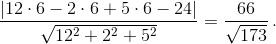
Ответ
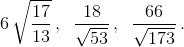
Чтобы оставлять комментарии, войдите или зарегистрируйтесь