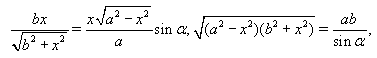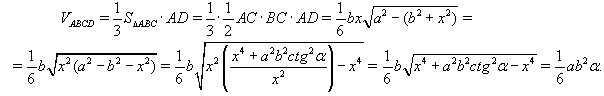Олимпиадная задача по стереометрии: объём треугольной пирамиды для 10-11 класса
Задача
Все грани треугольной пирамиды – прямоугольные треугольники. Наибольшее ребро равно a, а противоположное ребро равно b. Двугранный угол при наибольшем ребре равен α. Найдите объём пирамиды.
Решение
Пусть D – вершина данной треугольной пирамиды ABCD. Предположим, что у прямоугольных треугольников ADB, BDC и CDA прямые углы при вершинах A, B и C. Тогда AD < BD < CD < AD, что невозможно. Значит, прямые углы двух боковых граней прилежат к одной из вершин основания. Пусть это вершина A, т.е. ∠BAD = ∠CAD = 90°. Положим для определённости, что ∠BCD = 90°.Ребро DA – перпендикуляр к плоскости ABC. По теореме о трёх перпендикулярах ∠ACD = 90°, значит, BD > AB > BC, BD > AB
AC, BD > AD, т.е. BD наибольшее ребро пирамиды, BD = a, а AC = b.Пусть CK и CL – высоты прямоугольных треугольников ABC и BCD. Тогда CK ⊥ AB и CK ⊥ BD, поэтому CK – перпендикуляр к плоскости ABD, а KL ⊥ BD по теореме о трёх перпендикулярах, значит, CLK – линейный угол двугранного ребра при ребре BD. По условию задачи ∠CLK = α.Обозначим BC = x. Из прямоугольных треугольников ABC и BCD находим, что
а т.к. CK = CLsinα, то
откуда
Следовательно,
Ответ
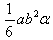
Чтобы оставлять комментарии, войдите или зарегистрируйтесь