Назад

Олимпиадная задача по планиметрии: доказательство неравенства KR и MQ в окружности

Задача 216491 • Сложность: 2 • 7-9 класс
Задача

В окружности с центром O проведена хорда AB и радиус OK, пересекающий её под прямым углом в точке M. На большей дуге AB окружности выбрана точка P, отличная от середины этой дуги. Прямая PM вторично пересекает окружность в точке Q, а прямая PK пересекает AB в точке R. Докажите, что  KR > MQ.

Разделы:
Планиметрия
Источники:
Окружная олимпиада (Москва) Олимпиады и турниры 2011 год 10 класс
Количество версий:
4
Решение

  Первый способ. Построим параллелограмм KRMN (рис. слева). Тогда  ∠NMQ = ∠KPQ = ∠NKQ  (второе равенство – теорема об угле между касательной и хордой). Следовательно, около четырёхугольника KNQM можно описать окружность. Так как угол NKM прямой, то MN – диаметр этой окружности, а MQ – хорда, отличная от диаметра. Поэтому  KR = MN > MQ.

               
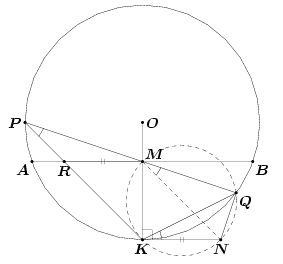
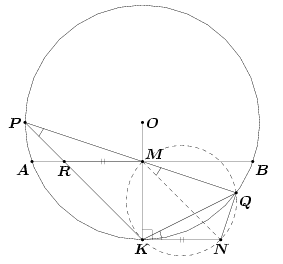
  Второй способ. Пусть точка K' диаметрально противоположна точке K (рис. справа). Тогда  ∠KRM = ∠PK'K   (как углы с соответственно перпендикулярными сторонами). Кроме того,  ∠PK'K = ∠PQK.  Рассмотрим точку R', симметричную точке R относительно KK', тогда

∠KR'M = ∠KRM = ∠PQK = ∠PK'K = ∠MQK,  значит, четырёхугольник KQR'M – вписанный.

  Дальнейшее аналогично описанному выше: KR' – диаметр, а MQ – хорда, отличная от диаметра.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет