Олимпиадная задача по планиметрии для 7–9 классов: доказательство равенства площадей
Задача
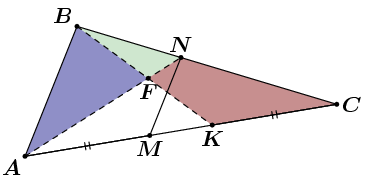
На сторонах AC и BC треугольника ABC выбраны точки M и N соответственно так, что MN || AB. На стороне AC отмечена точка K так, что CK = AM. Отрезки AN и BK пересекаются в точке F. Докажите, что площади треугольника ABF и четырёхугольника KFNC равны.
Решение
Пусть SABC = S. Тогда SABN : S = BN : BC = AM : AC = CK : AC = SBKC : S (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет