Олимпиадная задача по планиметрии: биссектрисы и равные отрезки в треугольнике
Задача
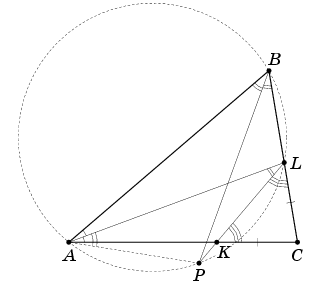
AL – биссектриса треугольника ABC, K – такая точка на стороне AC, что CK = CL. Прямая KL и биссектриса угла B пересекаются в точке P.
Докажите, что AP = PL.
Решение
Обозначим: ∠A = 2α, ∠B = 2β. Так как треугольник KCL – равнобедренный, то ∠KLC = ∠LKC = α + β. Отсюда ∠ALK = β, значит, четырёхугольник ABLP – вписанный. Следовательно, ∠LAP = ∠LBP = β = ∠ALP, то есть треугольник APL – равнобедренный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет