Олимпиадная задача про прыгающих блох и Пса Барбоса на доске 10×10 для 8–9 класса
Задача
На некоторых клетках доски 10×10 сидит по блохе. Раз в минуту блохи одновременно прыгают, причём каждая – в соседнюю клетку (по стороне). Блоха прыгает строго в одном из четырёх направлений, параллельных сторонам доски, сохраняет направление, пока это возможно, иначе меняет его на противоположное. Пес Барбос наблюдал за блохами в течение часа и ни разу не видел, чтобы две из них сидели на одной клетке. Какое наибольшее количество блох могло прыгать по доске?
Решение
Оценка. На одной вертикали может быть не более двух блох, прыгающих по вертикали (иначе блохи, находящиеся в клетках одного цвета, встретятся). То же верно для горизонталей. Итого на 20 горизонталях и вертикалях – не более 40 блох.
Пример. Ясно, что блохи с клеток разных цветов не смогут встретиться. Поэтому достаточно указать только 20 "белых" блох (расположение "чёрных" блох можно получить, например, симметрией относительно средней линии).
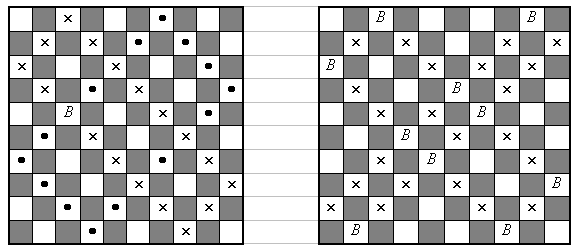
На левом рисунке нарисована одна "вертикальная" блоха В и все запрещённые положения "горизонтальных" блох (те, начиная с которых, "горизонтальная" блоха может оказаться с В на одной клетке). Как видим, запрещённые клетки образуют два прямоугольника, построенных на проходящих через В диагоналях. На правом рисунке размещены 10 "вертикальных" блох и все запрещённые ими положения "горизонтальных". Мы видим, что в каждой горизонтали осталась хотя бы одна незапрещённая белая клетка, куда можно посадить "горизонтальную" блоху.
Ответ
40 блох.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь