Олимпиадная задача Толпыго по комбинаторной геометрии для 8–9 классов: наименьшее число прямых в ломаной из 31 звена
Задача
На плоскости дана незамкнутая несамопересекающаяся ломаная, в которой 31 звено (соседние звенья не лежат на одной прямой). Через каждое звено провели прямую, содержащую это звено. Получили 31 прямую, некоторые, возможно, совпали. Какое наименьшее число различных прямых могло получиться?
Решение
Оценка. Кроме концов, на ломаной 30 вершин, и каждая является пересечением двух прямых. Если прямых не более восьми, то точек пересечения не более 7·8 : 2 = 28 – противоречие. Пример– на рисунке.
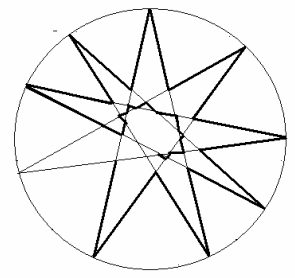
Ответ
9 прямых.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет