Олимпиадная задача по планиметрии для 10–11 классов: треугольник и шестиугольник

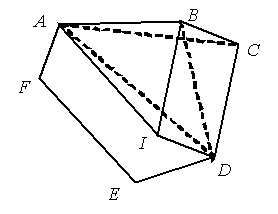
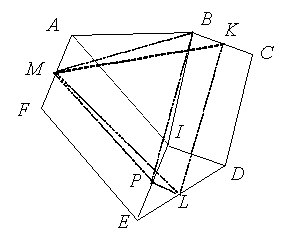
  Построим параллелограмм BCDI (см. рис.). По условию треугольники ABI и XYZ равны.   Первый способ. Пусть  S_XYZ = s,  S_ABCDEF = S,  K, L и M – середины соответственно сторон BC, DE и FA.

  Напомним, что если R – середина отрезка PQ, не пересекающего прямую HG, то   S_RHG = ½ (S_PHG + S_QHG)   (высота треугольника RHG, опущенная на HG, равна полусумме соответствующих высот треугольников PHG и QHG).

  Поэтому   S_KLM = ½ (S_BLM + S_CLM) = ¼ (S_BDM + S_BEM + S_CDM + S_CEM) = ⅛ (S_BDA + S_BDF + S_BEA + S_BEF + S_CDA + S_CDF + S_CEA + S_CEF).

  Заметим, что  S_DAB = S_CAB + S_IAB = S_CAB + s  (высота треугольникаADB, опущенная наAB, равна сумме соответствующих высот треугольниковACBиAIB).   Аналогично  S_EAB = S_FAB + s,   S_ACD = S_BCD + s,   S_FCD = S_ECD + s,   S_BFE = S_AFE + s,   S_CFE = S_AFE + s.   Отсюда  S_KLM= ⅛ (S_BDA + S_BDF + S_BEA + S_BEF + S_CDA + S_CDF + S_CEA + S_CEF) =  Заметим, что  S_BDF + S_ABF + S_BCD + S_DEF = S_AEF + S_CDE + S_ACE + S_ABC = S.   Поэтому  S_KLM= ⅛ (6s+ 2S) = ¼ (3s + S) >s.   (ТочкаIочевидно находится внутри шестиугольника, поэтому  s<S).   Второй способ.   Значит, отрезокAIпараллелен и равенFE, то естьAIEF– тоже параллелограмм.   ПустьP– серединаEI. Тогда  S_KLM > S_MPB > S_ABI = S_XYZ.   Оба неравенства следуют из следующего очевидного утверждения.  Пусть TUVW – параллелограмм, точка R и отрезок VW лежат по разные стороны от прямой TU. Тогда   S_RVW > S_RTU. (В первом случае используется параллелограммBKLP, во втором –AIPM.)

Ответ задачи отсутствует